Summary
I am close to retirement, at least in my research activity. Therefore I would like to summarize my scientific results made over last 25 years in immigration in Canada and later in the USA. I was trained and educated as a researcher, however, I have never been a full time scientist professionally. Most of my scientific results have been obtained in my leisure time. I am proud that my research projects have been done in collaboration with many outstanding scientists who found attractive to work with me on ideas that mainly I proposed.
- Optical Temporal Differentiator
In collaboration with Prof. Jose Azana at INRS in Montreal, Canada, we proposed and later designed and experimentally demonstrated an ultra-fast optical temporal differentiator based on Long Period Fiber gratings. Later, in collaboration with Technion, Israel, we produced a design of optical differentiator based on a fiber Bragg grating.
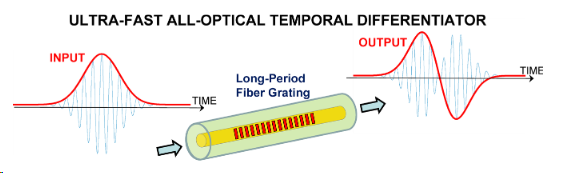
The implementation of all-optical circuits for computing, information processing, and networking could overcome the severe speed limitations currently imposed by electronic-based systems. A promising approach toward the implementation of ultrafast all-optical circuits is to emulate the developments in the electronic domain, i.e., to follow similar component and design strategies, using photonic technologies. For this purpose, the photonics counterparts of the fundamental devices that form “basic building blocks” in electronic circuits need to be designed and realized. In electronics, most of basic functionalities like logic operations, differentiation, and integration can be realized using a combination of operational amplifiers, resistors, and capacitors; however, there were still no photonic equivalents to these electronic components. Hence, the design and implementation of these photonic building blocks is a primary step toward the practical realization of all-optical information processing and computing circuits. A very relevant example of these fundamental devices is a photonic temporal differentiator.
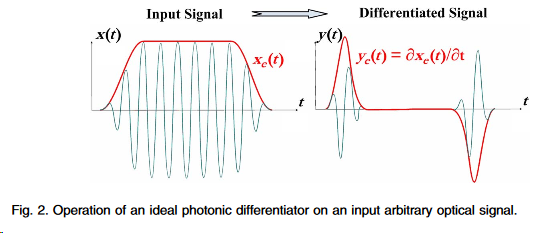
An N-th-order (N=1;2;3;..) photonic temporal differentiator is a device that provides, at its output, the N-th time derivative of the complex envelope of an input arbitrary optical waveform.
Photonic time differentiators were first proposed and theoretically investigated by Ngo et al.. This team designed arbitrary-order photonic differentiators using integrated-optic transversal filter topologies. To be more concrete, the designs first reported were based upon finite-impulse-response (FIR) optical digital filters. For instance, it was shown that a first-order photonic differentiator could be implemented using an asymmetric two-arm interferometer (two-tap FIR filter); this device provides the spectral response that is required for optical differentiation over a limited bandwidth centered at any of the destructive resonance frequencies of the interferometer and extending over a fraction of the device free spectral range (FSR) (inversely proportional to the relative delay between the interferometer arms). As an extension of this basic idea, higher order differentiators can be implemented by simply concatenating in series the corresponding number of identical two-arm interferometers. A large number of subsequently developed photonic differentiators both for complex-field optical waveforms and for intensity signals are based on this general concept.
Following this pioneer work, we found out that first-order time differentiation could be inherently provided by a simple uniform long-period fiber grating (LPG) operating in full-coupling condition. By ”uniform” we refer to the simplest possible grating profile, having an amplitude and period that are both constant along the whole grating length. An LPG allows light coupling between the guided mode and cladding modes in a single-mode fiber, thus resulting in a series of spectrally broad attenuation (resonance) bands centered at discrete wavelengths (frequencies) in the fiber transmission spectrum. The term “long” refers to its period, which typically varies from tens to hundreds of micrometers, as opposed to short-period fiber gratings (fiber Bragg gratings (FBGs), where the light is backscattered, resulting in coupling between modes traveling in opposite directions (in a Bragg geometry, the corrugation period is approximately half the optical wavelength, in micrometers or less).
The original proposal of a simple uniform LPG for optical differentiation has inspired a significant amount of subsequent work on the design and realization of ultrafast photonic temporal differentiators and integrators based on fiber-grating devices (both LPGs and FBGs). The advantages of fiber gratings are intrinsic to their all-fiber geometry, namely simplicity, relatively low cost, low losses, and full compatibility with fiber optic devices and systems. Additionally, fiber-grating concepts could be transferred to integrated-optic platforms, as desired for the future development of monolithic ultrafast all-optical processing circuits. Moreover, LPG and FBG technologies have attracted considerable interest over the last years due to their very wide range of applications in fiber-optic telecommunication systems, ultrafast optical pulse processing and shaping, and optical sensing; as a result, fiber-grating technologies have reached a high level of maturity, and efficient and advanced design and fabrication methods are now readily available. It should be mentioned that volume Bragg gratings have also been recently explored for optical differentiation as an interesting alternative to all-fiber gratings for high-power applications.
Besides its simplicity, a very attractive feature of an LPG-based differentiator is the large processing bandwidth practically attainable with this solution, namely, in the terahertz range. LPG differentiators can thus easily process optical signal with time features down to the sub-picosecond range. The first experimental demonstration of an ultrafast all-optical differentiator was based on this solution. Reflection FBGs, e.g., phase-shifted FBGs, sampled FBGs designed according to a reconstruction-equivalent-chirp method, and apodized FBGs designed by general layer-peeling synthesis algorithms, can be tailored to achieve the spectral responses that are necessary for first-order and higher order optical differentiators; however, besides requiring the use of nonuniform grating profiles, the resulting FBG designs are practically limited to processing bandwidths that are typicallyG50 GHz. Solutions based on especially apodized linearly chirped FBGs (LC-FBGs) have been explored to overcome the severe bandwidth limitations of conventional FBG designs.
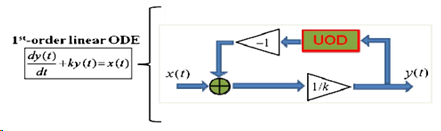
Fig. 1. Analog all-optical computing schemes for real-time solving of a first-order linear ODE using an ultrafast optical differentiator.
In analogy with their electronic counterparts, photonic temporal differentiators are key elements to create a large variety of information processing and computing platforms. A very relevant example of application of these fundamental devices is that of analog computing systems devoted to solving ordinary differential equations (ODEs). These equations play a central role in virtually any field of science or engineering, e.g., physics, chemistry, biology, economics, medical sciences, and the different branches of engineering. It is well known that linear ODEs can be solved in real time using a suitable combination of temporal differentiators, adders, and multipliers (amplifiers/attenuators). The possibility of realizing these computations all-optically translates into potential processing speeds well beyond the reach of present electronic digital or analog computers. Fig. 1 illustrates an example of all-optical computation of a constant-coefficient linear first-order ODE using either a first-order ultrafast optical differentiator (UOD in the figure). Notice that this simple differential equation actually models a number of important engineering systems and physical phenomena, including problems of motion subject to acceleration inputs and frictional forces, temperature diffusion processes, response of different RC circuits, population dynamics in biology and economy, etc. Beyond their intrinsic importance for general optical computing and information processing tasks, photonic differentiators implement fundamental mathematical operations on ultrafast optical temporal waveforms, thus being of interest for a wide range of applications, including optical/microwave pulse shaping, ultrafast optical control and sensing, ultrahigh-speed photonic coding and decoding, ultrafast optical signal measurements, photonic device characterization, implementation of optical memory units, etc.
2. PT-symmetry
A recent class of synthetic optical materials is that inspired by the concepts of parity (P) and time reversal (T) symmetries. This term came to optics from quantum physics after pioneering work of Carl Bender et al in 1998 where they suggested a hypothetical non-Hermitian extension of quantum mechanics, in which the postulate of Hermiticity of the underlying Hamiltonian is replaced by PT symmetric invariance. In the so-called unbroken PT phase, the Hamiltonian shows an entirely real energy spectrum in spite of being non-Hermitian.
Although the impact of PT-symmetry in quantum mechanics is still discussed, its notions have been successfully extended and observed in optics by utilizing the isomorphism between the Schrödinger equation in quantum mechanics and the wave equation in the paraxial approximation. It turned out that the grating profile proposed by Poladian in 1996 can be perfectly characterized as a PT-symmetric optical structure, with its complex refractive index obeying n(z) = n*(-z), i.e. even/odd symmetry for real/imaginary parts of the refractive index.
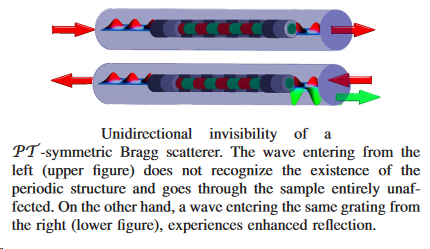
Poladian applied modal analysis, well established for theoretical description of linear waveguides with a variety of cross-sections, to study linear gratings in waveguides. Using this analysis, he demonstrated theoretically a nonreciprocal reflective behavior when the grating profile combines index and gain/loss modulations. Such a structure has different reflection spectra when viewed from opposite ends. At the same time it was emphasized that the transmission through the structure must be the same from both sides, and in a strict sense such gratings do not satisfy the Lorentz reciprocity condition, so that devices such as optical isolators cannot be designed purely on the basis of such gratings. Unidirectional invisibility in optical PT-symmetric structures
- Unidirectional invisibility in optical PT-symmetric structures
My team at McGill University studied the proposed grating design using Kogelnik’s coupled wave theory for waveguide gratings with index and gain/loss modulation. Such a configuration is realized when the index and gain/loss gratings overlap in the waveguide, and have the same period, but are shifted by a half period in respect to one another: . Perfect reflection asymmetry is achieved when the gratings have the same amplitude (a = b). In such a case the complex perturbation profile becomes a pure phase: ~exp (jkz). Our study theoretically demonstrated for the first time that the grating is not only transparent, as Poladian stated, but, in fact, light passing from one side of the grating does not change its amplitude or phase: such a behavior is classified as unidirectional invisibility. This result was published in 2005 in Optics express. Unfortunately, I have not had enough vision at that time to estimate an importance of this result and submit our paper to higher impact ratio journal. It was done only in 2011in Phys Rev, Lett by Z. Lin et al., six years later. However, my paper in Opt. Express is still one of my highly cited publications.
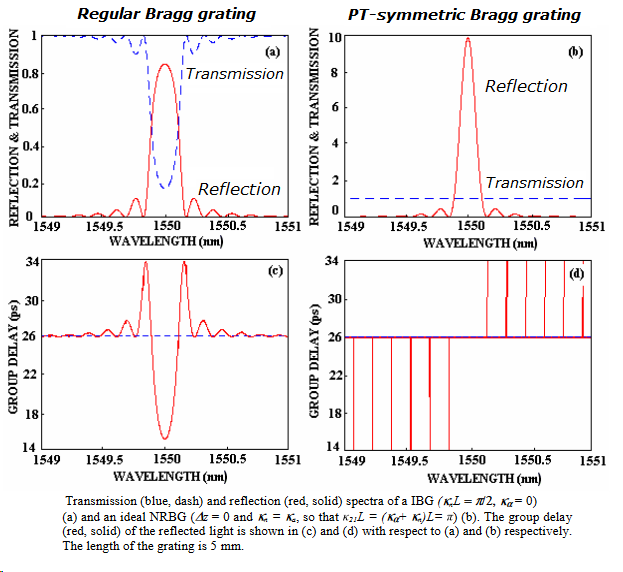
- Intrinsically single-mode longitudinal lasers based on PT_symmetry
PT symmetry has inspired several methods of mode selection in integrated semiconductor lasers. In particular, in semiconductor lasers stable unidirectional laser emission can be forced by using a complex grating near the symmetry breaking point. This provides a rather unique means to obtain unidirectional oscillation without resorting to non-reciprocal elements, such as optical diodes, which is impossible in the micro/nano scale. The complex grating does not break time reversal symmetry, however the asymmetric feedback between clockwise and counter-clockwise modes induces laser dynamics to suppress one of the two circuiting modes. My team was the first one to show this in the case of Distributed Reflector Gratin (DBR) lasers.
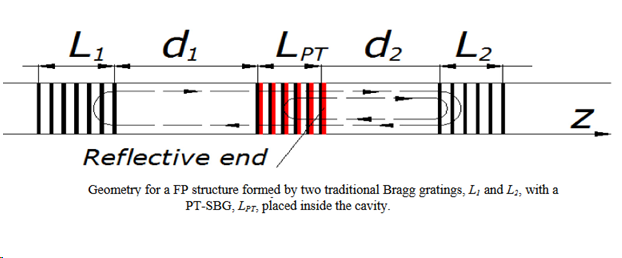
In traditional DBR lasers the length of amplifying cavity between the reflectors is proportional to a number of longitudinal modes. If this amplifying area with uniform gain is replaced by PT-symmetric balanced grating, then such a structure supports only one mode, the rest is suppressed
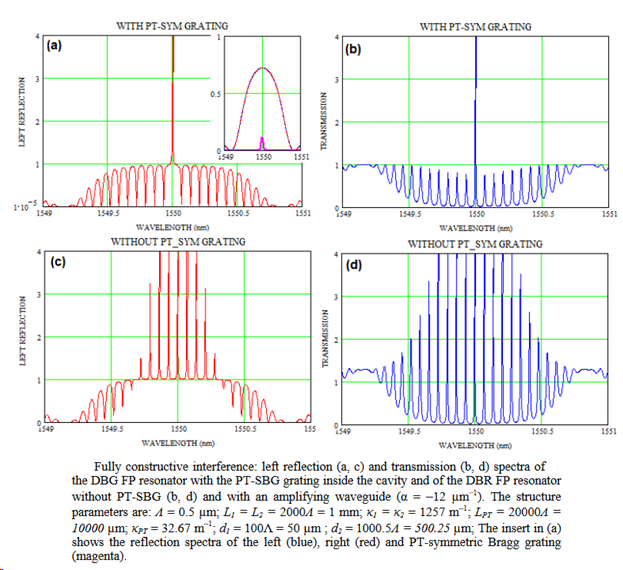
The method is robust against nonlinear instabilities that are known to set in in semiconductor lasers with slow carrier dynamics and a large linewidth enhancement factor. This DBR design can be significantly simplified with ability to use this simplified structure as a vertical emitting cavity or a horizontal one.
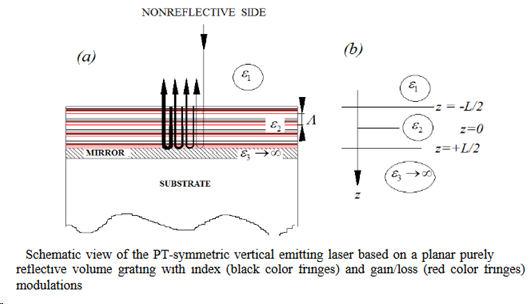
Another point to emphasize is that the lasing process of the gain/loss-dominated grating is very different from those of traditional gain-coupled DFBs described by Kogelnik and Shank. They demonstrated that after the first lasing condition occurs at the Bragg resonance (δ = 0) at the threshold κL=π/2, the next order lasing takes place at two frequencies symmetrical about the Bragg frequency (δ≠0) at κL=3π/2. In contrast to this lasing pattern, the proposed structure even in its gain/loss-dominated form always lases at the Bragg wavelength with significant mode discrimination, three times better than for the traditional gain coupled DFB structure.
RESEARCH CONTRIBUTIONS
h-index -20; i10-index-35
- H.F Jones, Mykola Kulishov, “Solitons in PT-symmetric grating-assisted co-directional coupler”, Journal of Physics: Conference Series 2038 (1), 012015, 2022.
- Bernard Kress, Mykola Kulishov, 2017, “Parity-Time Symmetry in Free Space Optics” in “Micro- and Nanophotonic Technologies”, Editors: Patric Meyrueis, Kazuaki Sakoda and Marcel Van de Voorde, Publisher: Wiley-VCH, Chapter 8; Pages: 143-192, ISBN: 978-3-527-34037-8 [Link].
- Mykola Kulishov, Bernard Kress, 2017, “Parity-Time Symmetric Cavities: Intrinsically Single-Mode Lasing” in “Micro- and Nanophotonic Technologies”, Editors: Patric Meyrueis, Kazuaki Sakoda and Marcel Van de Voorde, Publisher: Wiley-VCH, Chapter 9; Pages: 193-232, ISBN: 978-3-527-34037-8. [Link]
- H.F. Jones, M. Kulishov, B. Kress, 2016, “Parity time-symmetric vertical cavities: intrinsically single-mode regime in longitudinal direction“, Optics Express, Vol. 24, No. 14, 17125-17137, 2016, Citation: 5, [Link]
- H.F. Jones, M. Kulishov, “Extension of analytic results for a PT symmetric structure“, Journal of Optics, Vol. 18, 055101, 2016, Citation: 6, [Link].
- M. Kulishov, H.F. Jones, B. Kress, “Analysis of unidirectional non-paraxial invisibility of purely reflective PT-symmetric volume gratings”, Optics Express, Vol. 23, No.14, 18694-18711, 2015, Citation: 15, [Link].
- M. Kulishov, H.F. Jones, B. Kress, “Analysis of PT-symmetric volume gratings beyond the paraxial approximation” Optics Express, Vol. 23, No.7, 9347-9362, 2015, Citation: 30, [Link].
- M. Kulishov, B. Kress, H.F. Jones, “Novel optical characteristics of a Fabry-Perot resonator with embedded PT-symmetrical grating” Optics Express, Vol. 22, No.19, 23164-23181, 2014, Citation: 16, [Link].
- “Long-Period Fiber Gratings in Active Fibers” David Krčmařík, Mykola Kulishov and Radan Slavík, Chapter 5 in “Current Trends in Short- and Long-period Fiber Gratings”, book edited by Christian Cuadrado_Laborde, ISBN 978-953-51-1131-3, Citation: 2, Published: May 15, 2013.
- M. Kulishov, B. Kress, R. Slavik, “Distributed Bragg reflection structures based on PT-symmetric coupling with lowest possible lasing threshold”, Optics Express, Vol. 21, No.19, 23227-22337, 2013, Citation: 43, [Link].
- M. Kulishov, B. Kress, R. Slavik, “Resonant cavities based on Parity-Time-symmetric diffractive gratings”, Optics Express, Vol. 21, No.8, 9473-9483, 2013, Citation: 46, [Link].
- M. Kulishov, B. Kress, “Free space diffraction on active gratings with balanced phase and gain/loss modulations” Optics Express, Vol. 20, No.28, 29319-29328, 2012, Citation: 34, [Link].
- R. Slavik, Y. Park, M. Kulishov, J. Azana, “Terahertz-bandwidth high-order temporal differentiators based on phase-shifted long-period fiber gratings”, Optics Letters, Vol. 34, No. 20, 3116-3118, 2009, Citation: 75, [Link].
- D. Krcmarik, R. Slavik, M. Karasek, M. Kulishov, “Theoretical and Experimental Analysis of Long-Period Fiber Gratings Made Directly Into Er-Doped Active Fibers”, Journal of Lightwave Tech.,Vol. 27, No.13, pp. 2335-2342, 2009, Citation: 13, [Link].
- R. Slavik, M.Kulishov, Y. Park, J. Azana, “Long-period-fiber grating-based filter configuration enabling arbitrary linear filtering characteristics”, Optics Letters, Vol. 34, No. 7, 1045-1047, 2009, Citation: 24, [Link].
- D. Krcmarik, R.Slavic, Y. Park, M. Kulishov, J. Azana, “First-order loss-less differentiators using long period gratings made in Er-doped fibers”, Optics Express, Vol.17, No.2, pp.461-471, 2009, Citation: 10, [Link].
- M. Kulishov, D. Krcmarik, R. Slavik, “Design of terahertz-bandwidth arbitrary-order temporal differentiators based on long-period fiber gratings”, Optics Letters, Vol.32, No.20, pp.2978-2980 (2007), Citation: 48, [Link].
- M. Kulishov, J. Azana, “Design of high-order all-optical temporal differentiators based on multiple-phase-shifted fiber Bragg gratings”, Optics Express, Vol.15, No.10, pp.6152-6199 (2007), Citation: 92, [Link].
- R. Slavik, M. Kulishov, “Active control of long-period grating based filters made in erbium-doped optical fibers”, Optics Letters, Vol.32, No.7, pp.757-759 (2007), Citation: 13, [Link].
- N.K. Berger, B. Levit, B. Fisher, M. Kulishov, D.V. Plant, J. Azana, “Temporal differentiation of optical signals using a phase-shifted fiber Bragg gratings”, Optics Express, Vol.15, No.2, pp.371-381 (2007), Citation: 204, [Link].
- J.M. Laniel, M.Kulishov, N. Belanger, J. Azana, D.V. Plant “Comprehensive modeling of the stationary and dynamic behavior of imaginary Bragg gratings around threshold”, Optics Commnications, Vol. 269 pp.14-23 (2007).
- Y. Park, M.Kulishov, R. Slavik, J. Azana, “Picosecond and subpicosecond flat-top waveform generation using a single uniform long-period fiber grating”, Optics Express, Vol. 14, No.26, pp.12670-12678 (2006), Citation: 123, [Link].
- R. Slavik, Y. Park, M. Kulishov, R. Morandotti, J. Azana, “Ultrafast all-optical differentiator”, Optics Express, Vol.14, No.22, pp.10699-10707 (2006). Citation: 236, [Link].
- J.Azana, M.Kulishov, “All-fiber ultrafast optical differentiator based on π phase shifted long-period gratings”, Elect. Lett., Vol.41, No. 25 pp.1368-1369 (2005), Citation: 21, [Link].
- M.Kulishov, J.Azana, “Long-period fiber gratings as ultrafast optical differentiators”, Optics Letters, Vol.30, No.20, pp.2700-2702 (2005), Citation: 161, [Link].
- M.Gaidi, L.Stafford, J.Margot, M.Chaker, R. Morandotti, M.Kulishov, “Microfabricated SrTiO3 ridge waveguide”, Applied Physics Letters, Vol.86, pp.221106-1-3 (2005), Citation 19, [Link].
- M. Kulishov, J.Azana, “Ultrashort pulse propagation in uniform and nonuniform waveguide long-period gratings”, Journal of Optical Society of America A, Vol.22, No.7, pp.1319-1333 (2005), Citation 20, [Link].
- M.Kulishov, J.M. Laniel, N. Belanger, D.V. Plant, “Trapping light in a ring resonator using a grating assisted coupler with asymmetric transmission”, Optics Express, Vol.13, No.9, pp.3567-3578 (2005), Citation 44, [Link].
- M. Kulishov, J.M. Laniel, N.Belanger, J. Azana, D.V. Plant, “Nonreciprocal waveguide Bragg gratings”, Optics Express, Vol.13, No.8, pp.3068-3078 (2005), Citation 258, [Link].
- J. Azana, M. Kulishov, “Optical pulse shaping capabilities of grating-assisted codirectional couplers”, Microelectronics Journal, Vol.36, pp.289-293 (2005), Citation 4, [Link].
- M. Gaidi, L.Stafford, A.Amasian, M.Chaker, J.Margot, L.Martinu, M.Kulishov, “Influence of the microstructure on the optical characteristics of SrTiO3 thin films”, J.Mater.Res., Vol.20, No.1, pp.68-74 (2005), Citation 13, [Link].
- M. Kulishov, V.Grubsky, J.Schwartz, X.Daxhelet, D.V. Plant, “Tunable waveguide transmission gratings based on active gain control”, IEEE J. of Quantum Electronics, Vol.40, No.12, (2004), Citation 25 , [Link].
- M. Kulishov, J. Azana, “Ultrashort pulse propagation in grating-assisted codirectional couplers”, Optics Express, Vol.12, No.12, pp.2699-2709 (2004), Citation 3, [Link].
- M. Kulishov, X. Daxhelet, M. Gaidi, M. Chaker, “Transmission spectrum reconfiguration in long-period gratings electrically induced in Pockels-type media with the help of a periodical electrode structure”, IEEE J.Lightwave Techn., Vol. 22, N.3, pp.923-933 (2004), Citation 21, [Link].
- M. Gaidi, A. Amasian, M.Chaker, M.Kulishov, L. Martinu, “Pulsed laser deposition of PLZT films: structural and optical characterization,” Applied Surface Science, Vol.226, 347-354 (2004), Citation 66 , [Link].
- X. Daxhelet, M. Kulishov, “Theory and practice of long-period gratings – when a loss becomes a gain”, Optics Letters, Vol.28, N.9, 686-688 (2003), Citation 54, [Link].
- M. Kulishov, X. Daxhelet, “Reconfigurable π-shifted and Mach-Zehnder bandpass filters on the basis of electro-optically induced long-period gratings in a planar waveguide”, IEEE Journal of Lightwave Technology, Vol.21, N3, 854-861 (2003), Citation 10, [Link].
- M. Kulishov, X. Daxhelet, M. Gaudi, M. Chaker, “Electronically reconfigurable superimposed waveguide long-period gratings”, J. Opt. Soc. Am. A, Vol.19, N8, 1632-1648, (2002), Citation 21, [Link].
- M.Kulishov, X. Daxhelet, “Electro-optically reconfigurable waveguide superimposed gratings”, Optics Express, Vol.9 N10, 483-489, (2001), Citation 6, [Link].
- M. Kulishov, S. Sarkisov, Yu. Boiko, P. Cheben, “Switchable optical element with Bragg mode diffraction”, Optics Letters, Vol.26, N11, 759-751 (2001), Citation 13, [Link].
- M. Kulishov, P. Cheben, X. Daxhelet, S. Delprat, “Electro-optically induced tilted phase gratings in waveguides”, J. Opt. Soc. Am. B, Vol.18, N4, 457-464, (2001), Citation 14, [Link].
- M. Kulishov, “Tunable electro-optic microlens array. I. Planar geometry”, Applied Optics, Vol.39, N14, 2332-2339, (2000), Citation 15, [Link].
- M. Kulishov, “Tunable electro-optic microlens array. II. Cylindrical geometry”, Applied Optics, Vol.39, N20, 35093515, (2000), Citation 5, [Link].
- M. Kulishov, “Interdigitated electrode-induced phase grating with an electrically switchable and tunable period”, Applied Optics, Vol.38, N36, 7356-7363, (1999), Citation 16, [Link].
- M. Kulishov, “Adjustable electro-optic microlens with two concentric ring electrodes”, Optic Letters, Vol.23, N24, 1936-1938, (1998), Citation 12 [Link].
- M. Kulishov, “Modeling of a converging gradient-index lens with variable focal length in a lanthanum-modified lead zirconate titanate ceramic cylinder with lateral multielectrode structure”, Applied Optics, Vol.37, N16, 3506-3514, (1998), Citation 5, [Link].
- N.B. Kuleshov, S.S. Sarkisov, “Theoretical analysis of electrode raster performance in reliefographic spatial light modulators with signal recording at the substrate side”, Optics Communications, Vol. 91, 416-424, (1992).
